| Juno's Spinnerについて 1 | |
ホーム > 多面体おもちゃ > Juno's Spinner | |
| 上へ 次へ | |
| エレメントの条件 | |
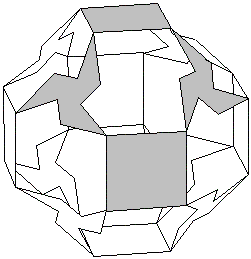
| Juno's Spinnerは球対称に配置された,いくつかの弾性のあるエレメントが,ハトメ等で止められ,その周りに自由に回転できるようになっている. 右の図は Juno's Spinner 6面体(立方体) |
 |
| ここでは平面上の4節リンク機構がいくつもつながったものとして考える. | 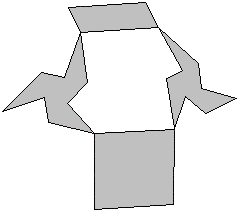 |
| 4節リンク機構では図のAを固定したときB,C等はAの端点の周りを一定の角度だけ回転することができるが,B,Cの回転する角度は一般には異なる. しかし,リンク機構が平行四辺形のときは,この角度が同じになる. | 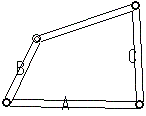 |
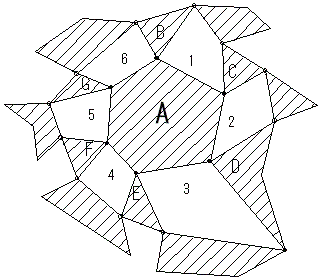
| 平面上で4節リンク機構が図のように1つのエレメントAを1周して閉じているとする. Aを固定したとき,周りのエレメントB〜Gが動くことができる条件は何か? 最も簡単な例は,四辺形1〜6がすべて平行四辺形になっていることである. それはエレメントB〜Gの回転角がすべて同じになり,全体として矛盾なく動くことができるからである. |
 |
| 多くのJuno's Spinnerで上の「平行四辺形条件」が成り立っているが,エレメントに弾力性があるため,絶対条件とはいえない. | |
| 上へ 次へ | |
[ホーム] [幾何学おもちゃ] [多面体おもちゃ] [Java Applet] [Links] [更新情報] |